矩阵求导术
自定义Triton算子,需要在实现反向传播时给出相应的梯度计算方法,梯度表达式的推导过程涉及矩阵求导的运算法则。
下面以flash-linear-attention为例,介绍一下flash-linear-attention的实现方法,顺便推导一下梯度的计算过程。
Forward
标准attention:
train:并行,高效 \[ \begin{align*} \rm Q, \rm K, \rm V &= \rm XW_Q, \rm XW_K, \rm XW_V, \\ \rm O &= \ softmax\big((\rm Q \rm K^\intercal) \odot \rm M \big) \rm V, % \end{align*} \] where \(\rm X \in R^{L \times d}\),\(W_Q, W_K, W_V \in R^{d \times d}\), \(\rm M \in \{-\infty,1\}^{L \times L}\) , \(\rm M_{ij}=1\) if \(i\ge j\) and \(\rm M_{ij}=-\infty\) if \(i<j\). (Here we assume a single attention head for simplicity.)
inference:串行,kv cache \[ \begin{align*} q_t, \ k_t, \ v_t &= x_t W_Q, \ x_t W_K, \ x_t W_V, \\ o_t &= \frac{\sum_{i=1}^{t} \exp(q_t k_i^\intercal)v_i}{\sum_{i =1} ^{t} \exp(q_t k_i^\intercal)}, \end{align*} \]
Linear attention
replace \(\exp(q_t k_i^\intercal)\) with a kernel \(k(x, y) = \langle\phi(x), \phi(y)\rangle\)),since we have: \[ \begin{align*} o_t &= \frac{\sum_{i=1}^{ t}\phi(q_t)\phi(k_i)^\intercal v_i}{\sum_{i=1}^{t} \phi(q_t)\phi(k_i)^\intercal } = \frac{\phi(q_t) \sum_{i=1}^{t}\phi(k_i)^\intercal v_i}{\phi(q_t) \sum_{i=1}^{t}\phi(k_i)^\intercal}. % \end{align*} \] Letting \(\rm S_t=\sum_{i=1}^{t}\phi(k_i)^\intercal v_i\) and \(z_t=\sum_{i=1}^{t}\phi(k_i)^\intercal\) where \(\rm S_t \in \mathbb{R}^{d\times d}, z_t \in \mathbb{R}^{d\times 1}\), we can rewrite the above as an RNN: \[ \begin{align*} \rm S_t = \rm S_{t-1} + \phi(k_t)^\intercal v_t, \ z_t = z_{t-1} + \phi(k_t)^\intercal, \ o_t = \frac{\phi(q_t) \rm S_t}{ \phi(q_t) z_t}. \end{align*} \] recent work has found that a linear kernel (i.e., setting \(\phi\) to be the identity) without a normalizer works well in practice: \[ \begin{align} & \rm S_t = \rm S_{t-1} + k_t^\intercal v_t, \quad o_t = q_t \rm S_t. \end{align} \]
分块并行形式
for \(i \in [0, 1, \dots \frac{L}{C}-1]\): \[ \rm S_{[i+1]} = \rm S_{[i]} + \underbrace{\sum_{j=iC + 1}^{(i+1)C} k_{j}^\intercal v_{j}}_{\rm K^\intercal_{[i]}\rm V_{[i]}} \quad \hspace{1mm} \in \mathbb{R}^{d\times d}. \]
\[ \rm O_{[i+1]} = \underbrace{\rm Q_{[i+1]}\rm S_{[i]}}_{\text{inter-chunk}: \rm O^\text{inter}_{[i+1]}} + \underbrace{\big((\rm Q_{[i+1]}\rm K_{[i+1]}^{\intercal})\odot\rm M\big)\rm V_{[i+1]}}_{\text{intra-chunk}: \rm O^{\text{intra}}_{[i+1]}}, \]
算法流程如下:

Backward
 \[
\rm O = \rm Q_{[n]} \rm S +(\rm Q_{[n]} \rm K_{[n]}^\intercal \odot\rm
M)\rm V_{[n]}
\]
\[
\rm O = \rm Q_{[n]} \rm S +(\rm Q_{[n]} \rm K_{[n]}^\intercal \odot\rm
M)\rm V_{[n]}
\]
\[ \rm S = \rm S + \rm K_{[n]}^\intercal \rm V_{[n]} \]
输入:\(\nabla O\), 输出:\(\nabla Q\),\(\nabla K\),\(\nabla V\)
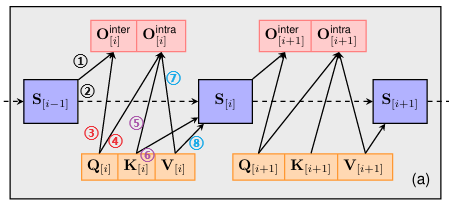
S, Q, K, V均有两个输出节点(即图中有两个向外的箭头),因此它们的梯度均由两部分构成:
S:
引理1: Y、A、X、B均为矩阵,若Y=AXB,则\[\nabla X = A^\intercal \nabla Y B^\intercal\]
根据该引理,我们有:
\[\nabla S_{①} \ = \rm Q_{[n]}^\intercal \nabla O\]
\[\nabla S_{②} \ = \nabla S^{'}(下一级S的梯度)\]
\[\nabla S = \nabla S_{①} + \nabla S_{②} \ = \rm Q_{[n]}^\intercal \nabla O + \nabla S\]
Q:
\(\nabla Q_{③} \ = \nabla O \ \rm S^\intercal\)
引理2: 矩阵链式求导的一般方法:借助矩阵的迹(trace)运算。
迹的定义:方阵的主对角线元素之和。
由迹的定义易得:
- 标量套上迹:\(a = tr(a)\)
- 转置: \(tr(A) = tr(A^T)\)
- 线性: \(tr(A±B) = tr(A) + tr(B)\)
- 矩阵乘法交换律:\(tr(AB)=tr(BA) = \sum_{i,j}A_{ij}B_{ij}^T = \sum_{i,j}A_{ij}B_{ij}\) ,即A和\(B^T\)(或B和\(A^T\))的内积
- 逐元素相乘:\(tr(A^T(B \odot C)) = tr((A \odot B)^T C) = \sum_{i,j}A_{ij}B_{ij}C_{ij}\)
矩阵链式求导: \(df = tr(\nabla Y^T dY) = tr(\nabla X^T dX)\)
故有:\[tr(\nabla O^T dO) \\= tr\big(\nabla O^T (dQ_{[n]}K_{[n]}^T \odot M)V_{[n]}\big) \\=tr\big(V_{[n]}\nabla O^T (dQ_{[n]}K_{[n]}^T \odot M)\big)\\=tr\big((\nabla OV_{[n]}^T \odot M)^TdQ_{[n]}K_{[n]}^T\big)\\=tr\big(K_{[n]}^T(\nabla OV_{[n]}^T \odot M)^TdQ_{[n]}\big)\\=tr\big(((\nabla OV_{[n]}^T \odot M)K_{[n]})^TdQ_{[n]}\big)\]
上述推导过程主要使用了迹的矩阵乘法交换律和逐元素相乘律,对照链式求导公式可得,\[\nabla Q_{④} = (\nabla OV_{[n]}^T \odot M)K_{[n]}\]
\[\nabla Q_{[n]} = \nabla Q_{③} + \nabla Q_{④} \ = \nabla O \ \rm S^\intercal + (\nabla OV_{[n]}^T \odot M)K_{[n]}\]
K、V:类似方法可得:
\[\nabla K_{[n]} = \nabla K_{⑤} + \nabla K_{⑥} \ = V_{[n]}\nabla S^T + (V_{[n]}\nabla O^T \odot M^T)Q_{[n]}\]
\[\nabla V_{[n]} = \nabla V_{⑦} + \nabla V_{⑧} \ = K_{[n]}\nabla S + (\rm Q_{[n]} \rm K_{[n]}^T \odot\rm M)^T \nabla O\]
具体算法流程:
